Epargner c’est renoncer à dépenser de l’argent aujourd’hui pour le dépenser dans un futur plus ou moins proche,
c’est différer sa consommation dans le temps. Si la valeur nominale de l’épargne peut être garantie contre une faible rémunération (livret A par exemple),
il subsiste deux risques : voire la valeur réelle de son argent se déprécier avec l’inflation et ne plus être en mesure de profiter de l’argent de son épargne.
Investir c’est acheter un produit financier (action, obligation) en espérant le revendre plus cher.
Le prix des produits financier varient au cours du temps et le risque de voir la valeur de son investissement réduite à zéro n’est pas négligeable.
Pour contrer ce risque, l’adage veut que l’on ne mette pas tous ses œufs dans le même panier :
il est préférable d’acheter plusieurs produits financiers suffisamment différents pour que les gains soient supérieurs aux pertes.
L’autre pratique à mettre en place est de régulièrement réajuster les actifs que l’on possède dans son portefeuille : en racheter certains, en vendre d’autres.
Cette page va montrer comment choisir la composition de son portefeuille et comment arbitrer régulièrement sa composition avec des outils développés en Python.
Note : En bourse un investisseur peut acheter des actions ou obligations de manière individuelle ou adhérer à un fond géré par des professionnels.
Dans ce dernier cas l’adhésion et le retrait prennent du temps car les gérants doivent calculer la valeur liquidative de la part de l’individu
pour augmenter le capital du fond ou le réduire. De plus, les frais de ces fonds sont élevés (2% du capital payable annuellement).
Il existe un produit financier nommé Exchange Traded Fund (ou ETF)
qui représente une part de fond à capital fixe et qui peut être vendu sur le marché comme une action,
c’est-à-dire immédiatement si un acheteur est présent. L’intérêt des ETF est qu’ils peuvent copier un indice boursier comme le CAC40 ou le SP500 et
il a été montré que
sur le long terme les fonds gérés par des professionnels ne font pas mieux que l’indice boursier de référence d’un pays.
Cet américain a révolutionné la gestion financière en 1952 en introduisant sa théorie moderne du portefeuille.
Le paradigme est de considérer non pas le prix des actifs mais leur rendement (variation du prix) et de considérer celui-ci comme une variable aléatoire.
Ainsi il est possible de calculer :
W = arg ( minimize( Vol(Rp) ) )
s.c. E(Rp) = Rmin
Ce type de problème mathématique se résoud bien avec la méthode des moindres carrés par exemple.
Il s'avère qu'en pratique la rentabilité des actifs ne suit pas une loi normale, ce qui rend la théorie fragile dans les faits.
Grâce à Python, à la librairie pandas et aux outils proposés dans le MOOC Investment Management with Python and Machine Learning disponible sur Coursera, nous allons étudier différents ETF dont les données ont été récupérées sur Curvo.eu. Nous avons récupéré les données mensuelles de plusieurs ETF :
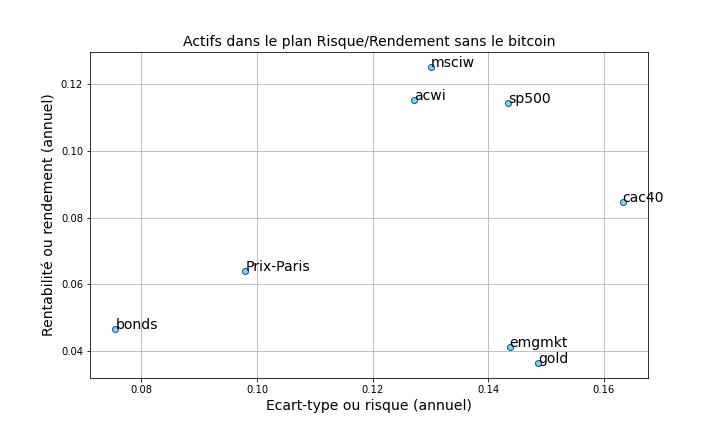
Pour chaque actif la série temporelle de prix est transformée en série de variations relatives, puis nous calculons l'espérance de rendement annuel et son écart-type annuel. Les résultats sont présentés dans le tableau ci-dessous :
| Actif | Espérance de rendement annuel | Ecart-type de rendement annuel |
|---|---|---|
| sp500 | 0,114 | 0,143 |
| cac40 | 0,085 | 0,163 |
| msciw | 0,125 | 0,130 |
| acwi | 0,115 | 0,127 |
| emgmkt | 0,041 | 0,144 |
| gold | 0,036 | 0,149 |
| btc | 1,132 | 1,665 |
| bonds | 0,047 | 0,075 |
| Prix-Paris | 0,064 | 0,98 |
Au delà du risque et du rendement de chaque actif pris individuellement, il est important de regarder la covariance des actifs entre-eux.
D'une part parce que la covariance renseigne sur le comportement des actifs, à la hausse et à la baisse : deux actifs réagissent-ils globalement de la même
façon au cours du temps ? D'autre part, la covariance rentre dans le calcul de l'écart-type du portefeuille. Nous sommes obligé d'exclure les prix de l'immobilier
parisien car il s'agit de variations annuelles, contre mensuelles pour les autres actifs.
Le calcul de la covariance de plusieurs actifs se représente aisément dans une matrice de covariance qui peut ensuite être normalisée en matrice de corrélation.
La figure C représente la matrice de corrélation des actifs.
Cette figure montre que les actifs représentatifs des actions, quelque soit le secteur géographique, sont fortement corrélés entre eux.
Mais à l'inverse les autres actifs sont peu corrélés entre eux et avec les actions.
Le recours à la matrice de corrélation montre que l'actif gold, peu corrélé avec d'autres actifs a son intérêt dans un portefeuille.
NB : Notons que l'analyse porte sur un temps assez court (11 ans) et que l'intervalle 2011 à 2021 correspond à une période de marché haussier pour les actions et baissier pour l'or.
A partir de l'algorithme d'optimisation développé dans le MOOC, nous réalisons plusieurs optimisations de Markowitz sur l'ensemble de nos actifs
(hors prix de l'immobilier parisien) et sur la période totale.
Nous faisons varier à chaque fois le rendement souhaité.
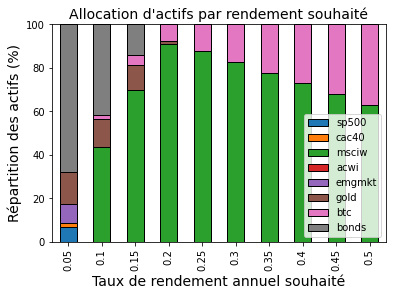
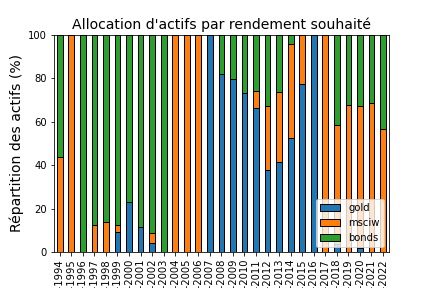
La figure D présente les allocations d'actifs en fonction du rendement souhaité.
Tant que le rendement souhaité est relativement faible, la répartition est un panachage de plusieurs actifs et hormis pour
un rendement de 5%, un seul type d'actif de la classe action est sélectionné : MSCIW.
Quand le rendement demandé commence à être important,
la répartition est un mixte de Bitcoin (dans le rendement est élevé) et
de MSCIW. Le fait que cet actif soit le seul à être sélectionné parmis les ETF actions
s'explique par le fait que tous les ETF actions sont fortement corrélés entre eux et MSCIW est celui qui présente le meilleur rendement pour un risque moindre que les autres (cf figure B).
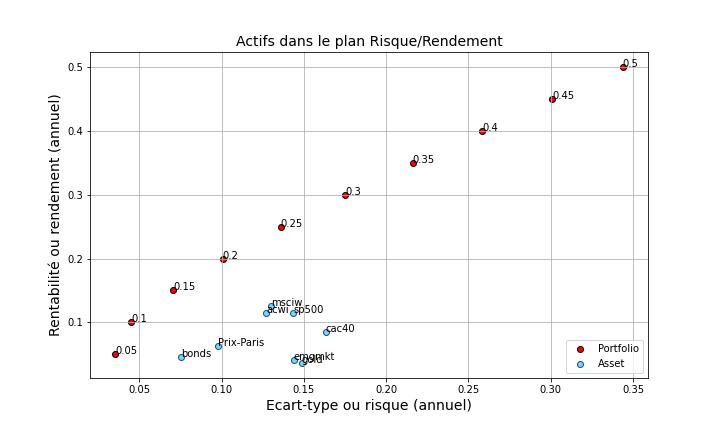
La figure E représente les différents portefeuilles générés par l'allocation de Markowitz et positionnés dans le plan risque/rendement des actifs.
Cette analyse nous enseigne que jusqu'à un rendement désiré de 25% le portefeuille est dans
une zone de risque similaire aux actions. Avec un rendement désiré de 20%, le risque du portefeuille est même inférieur à celui des ETF actions.
Nous venons de voir comment l'allocation de Markowitz permet de créer des portefeuilles optimisant risque et rendement. Néanmoins, l'allocation marche à posteriori et elle a été réalisée sur toute la période. Dans la réalité l'investisseur va décider d'un taux de rendement souhaité, il va calculer une allocation, investir, puis suivre son plan d'investissement au cours du temps. Nous avons développé un algorithme simulant une stratégie d'investissement au cours du temps :
Nous faisons plusieurs simulations en faisant varier conjointement les rendements annuels souhaités et la durée en années sur laquelle nous faisons l'allocation.
Concentrons sur une des simulations qui a donné les meileurs résultats : 10% de rendement souhaité et une période de 9 ans pour calculer les allocations de Markowitz.
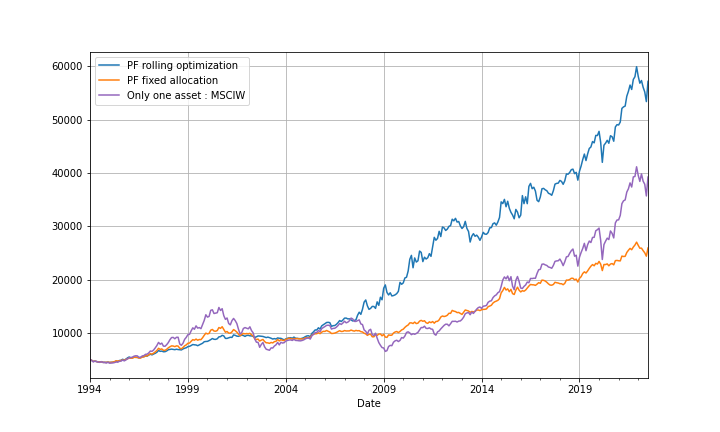
La figure J montre que cet investissement permet de passer de 5 000€ en 1994 à 60 000€ en 2022. Si l'on avait suivi une allocation fixe avec rééquilibrage
le montant atteint au bout de 28 ans aurait été de 25 000€ environ (nous parlons de montants nominaux), 40 000€ pour un investissement sur le seul MSCIW.
La figure K montre les compositions des portefeuilles au cours du temps avec la stratégie rolling optimization. Les changements d'allocations sont très brutaux.
Par exemple, après 3 ans investit en 100% MSCIW, l'algorithme recommande d'investir à 100% en or au 1er janvier 2007. C'est intéressant car c'est à la veille de la crise
des subprimes qui fit plonger la bourse et vis l'or monter (fait habituel en période de crise). Néanmoins, d'un point de vue psychologique il faut un certain courage pour suivre
une recommandation aussi brutale.
Quand nous regardons le cours des actifs relativement à la plus haute valeur atteinte (drawdowns - figure L), nous voyons qu'avec la stratégie rolling optimization nous chutons parfois de 15%, contre près de 55% pour l'investissement sur le seul actif MSCIW. Cela semble indiquer que la stratégie rolling optimization permet de se prémunir des chutes brutales de marchés.
Pour choisir dans quel actif investir, il est possible d'utiliser une méthode rationnelle cherchant à déterminer le meilleur compromis.
Pour ensuite gérer son investissement dans le temps il est aussi possible de recaluler l'allocation optimale sur une base régulière.
Néanmoins les résultats restent fragiles et aucune tendance ne se dessine, les résultats obtenus dépendent du scénario qui a été réalisé (cours historiques des actifs)
et il faut être prudent pour en déduire une quelconque méthode d'investissement.
Il pourrait être intéressant de simuler plusieurs scénarii pour le cours des actifs via un modèle basé sur le mouvement brownien : on pourrait ainsi évaluer nos stratégies
en terme de statistiques de réussite.